The content of this page has not been vetted since shifting away from MediaWiki. If you’d like to help, check out the how to help guide!
Overview
Even after correcting for fixed-pattern noise (see here), differences in brightness and contrast between images, e.g. due to bleaching, might persist and be visible in the fused images. To correct for this, we estimate optimal linear transforms of pixel intensities in adjacent images to achieve uniform brightness and contrast in the whole dataset. We minimize the intensity difference of all pixels in the overlapping volume of two images according to the current registrations via a linear transform for each image: \(I'(x) = I(x) * \alpha + \beta\)
The brightness and contrast adjustment is available in Multiview mode under Processing › Intensity Adjustment.
Calculating the intensity adjustment requires the images to be aligned, therefore use it as a last step after registration before fusing the dataset.
Usage
Clicking Compute… in the Intensity adjustment menu brings up the following dialog:
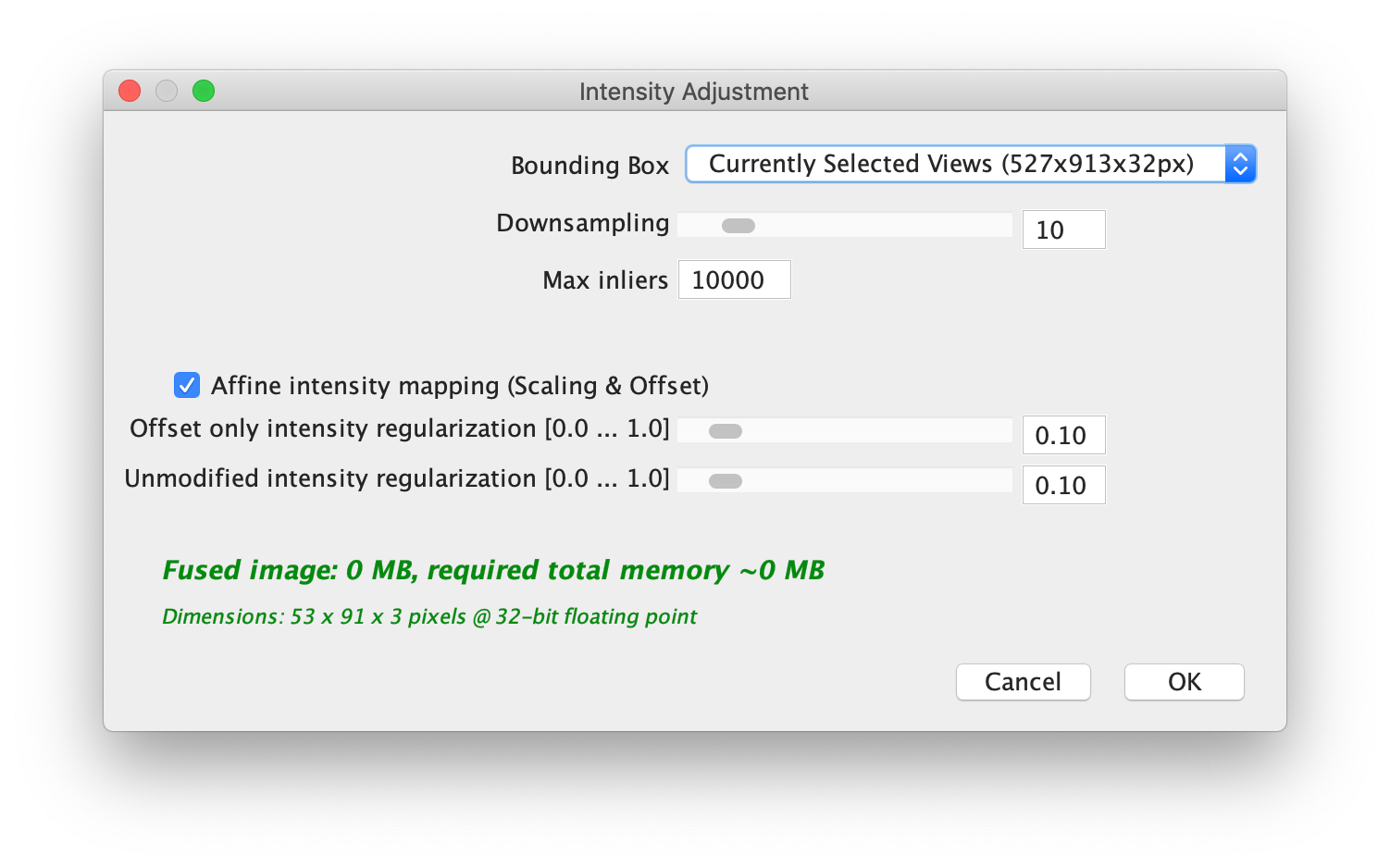
First, since the adjustment is calculates for pixel intensities in overlapping areas of the images, you can select how to load the pixels:
- Bounding Box specifies the area to load for the calculation. We will automatically determine overlapping areas in it. Note that the intensity adjustment can not be calculated for images not in the bounding box.
- Downsampling By how much to downsample the images for the calculation. Since in this step we are only interested in larger-scale intensity variations, we recommend to downsample a lot.
- Max inliers How much pixels to consider at most for each image pair.
Below, you can set various regularization parameters for the intensity adjustment function that is fitted to the data. In detail, we will fit a weighted average of the original image intensity \(I(x)\) and a weighted average of a linear transformation \(I(x) * \alpha + \beta1\) and an additive offset \(I(x) + \beta2\) with weights \(\lambda1\) and \(\lambda2\):
\[\lambda2 * I(x) + (1-\lambda2) * (\lambda1 * (I(x) + \beta2) + (1 - \lambda1) * (I(x) * \alpha + \beta1) )\]The options at the bottom of the dialog set the values for \lambda1 and \lambda2:
- Affine intensity mapping (Scale & Offset) enables a linear transform of the intensities instead of just an additive offset.
- Offset only intensity regularization corresponds to \(\lambda1\). Higher values give more weight to an offset-correction vs. a scale and offset correction. Note that if Affine intensity mapping is deselected, \(\lambda1 = 1\) automatically, so only an offset transform will be calculated.
- Unmodified intensity regularization corresponds to \(\lambda2\). Higher values give more weight to an identiy transformation, i.e. leaving the corrected intensity values as close to the original as possible.
If \(\lambda1\) and \(\lambda2\) are both set to 0, the fitted transformation might converge to \(I(x) * 0 + \beta1\), i.e. setting all intensities equal. To prevent this, please always use values \(\ge 0\) for at least one of the regularization parameters.
Displaying
Clicking List all in the intensity adjustment sub-menu will list the current intensity adjustment for each image in the dataset.
Removing
Clicking Remove in the sub-menu will remove the intensity adjustment from the currently selected image(s).
Go back to the main page