TrackMate

TrackMate is your buddy for your everyday tracking.

Citing TrackMate papers

Please note that TrackMate is available through Fiji, and is based on several publications. If you use it successfully for your research please be so kind as to cite our work:

doi:10.1038/s41592-022-01507-1

and / or

doi:10.1016/j.ymeth.2016.09.016

Presentation

Examples

TrackMate user-interface

TrackMate has a user-friendly interface that allows for performing tracking, data visualization, editing results and track analysis in a convenient way. TrackMate is distributed in Fiji, integrates well with ImageJ and Fiji tools, and does not require a complex installation procedure. TrackMate also has a component to display and annotate cell lineages: TrackScheme.

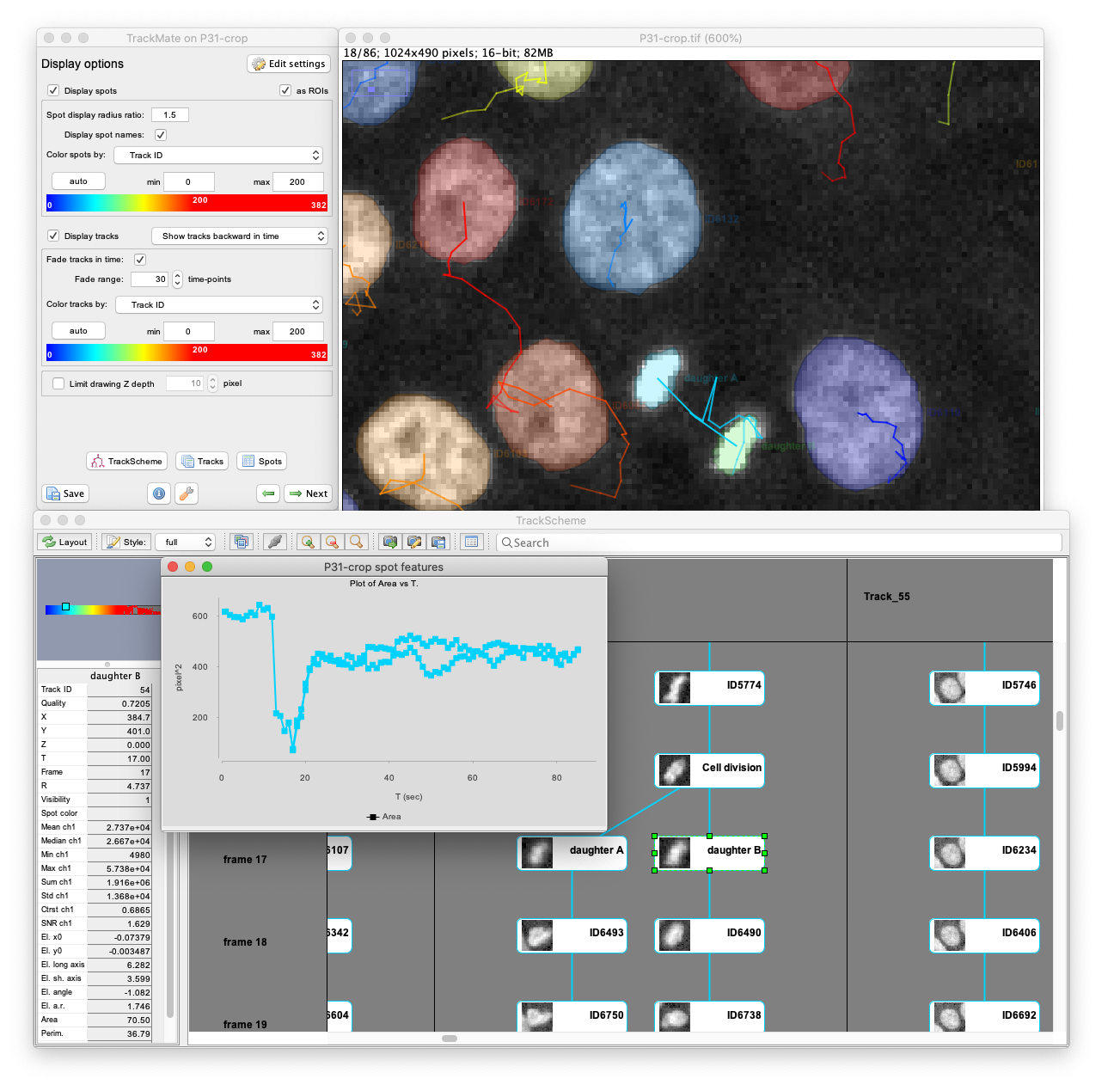
Using state-of-the-art segmentation algorithm

Starting with version 7, TrackMate can detect, store and exploit the object contours in 2D. Also, TrackMate integrates state-of-the-art segmentation algorithms, such as ilastik, MorphoLibJ, StarDist, and Weka. Below you can see migrating cells tracked with the StarDist detector implemented in TrackMate.

You can use these algorithms to track objects in various imaging modalities. For instance, here are T-cells imaged in bright-field tracked with a custom Deep Learning model used with StarDist:

Interfacing with external segmentation algorithms

TrackMate includes detectors that can create objects to track from a mask image, a label image or a probability map. This way we can interface with external segmentation algorithms, such as cellpose. Below are two movies segmented with cellpose. We exported the segmentation results as a label image, that we added to the raw image as a 2nd channel, then used in TrackMate for tracking. In the first one we follow mouse hematopoietic stem cells migrating in a hydrogel microwell:

And here we follow migrating cancer cells, stained for their membrane:

Tracking and lineaging cells in 3D

TrackMate works indifferently in 2D or 3D. Below is a movie showing the first 2 hours of a C.elegans embryo development, followed in 3D over time using TrackMate (strain: AZ212). (However, the object contour is displayed only for 2D images.)

Tracks with fusion, split and bridging gap events

Tracks with fusion, split and bridging gap events. TrackMate can be set to detect and deal with gap-closing events, splitting events and merging events.

Track analysis

TrackMate performs a number of measurements on the objects it tracks. These measurements can be browsed, exported and plotted from within the user interface.

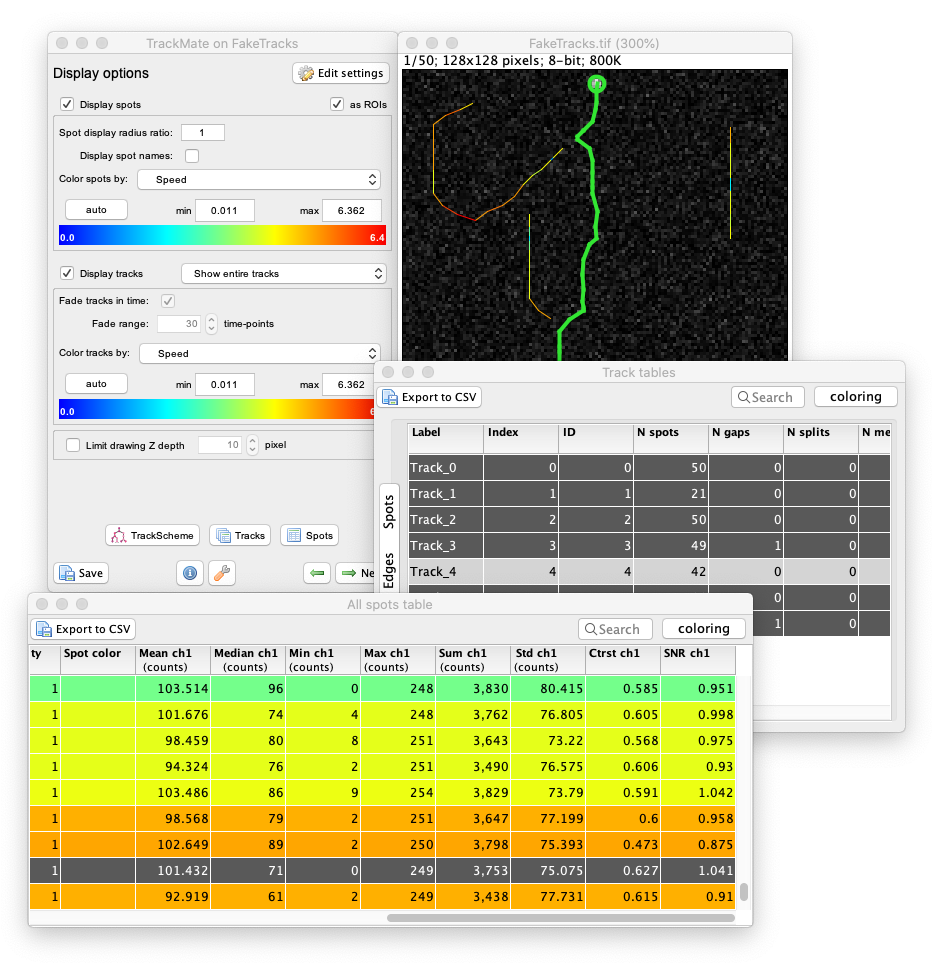
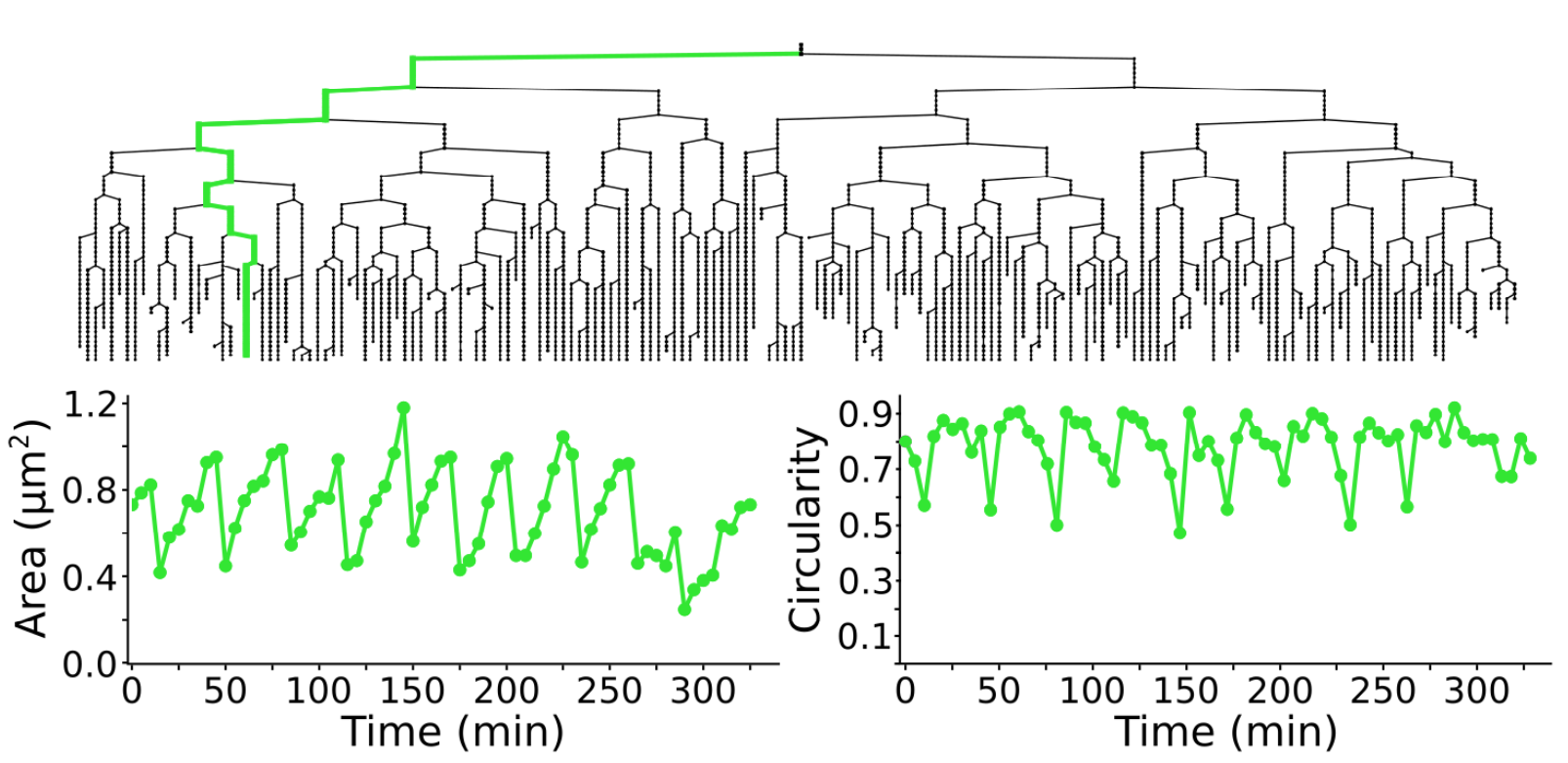
Measuring morohpological features over time

Following cell morphology over several divisions within a lineage. The lineage follows the growth of a Nesseiria meningitidis. The bottom graphs display the cell area and circularity for the cell highlighted in green in the above lineage. For 2D images, TrackMate can measure the morphological features of the objects it tracks.

Generating movies that follow a single cell over time

A movie following one cell of a C.elegans embryo tracked over 3 hours, as it divides. The track follows the lineage from cell AB to ABaraapap.

Segmenting objects in 3D with a slice-by-slice approach

TrackMate ships and integrates several nice Deep-Learning based and Machine-Learning based segmentation algorithms. They work especially well in 2D but we can also use them to segment 3D objects with TrackMate. The idea is to tell TrackMate “this is not a 3D image but a 2D+T image that you will track”. For instance you could use cellpose on the individual 2D slice to segment sections of the object, then merging the multiple 2D contours in a single 3D object. This is the resulting segmentation on a Drosophila melanogaster embryo:

And the same approach applied to Arabidopsis thaliana floral meristem:

Single Particle Tracking

TrackMate provides the tools to perform single particle tracking (SPT) typically in the context of microscopy. SPT is an image analysis challenge where the goal is to segment some objects and follow them over time. Each object is detected or segmented in multiple frames and its trajectory is reconstructed by assigning it an identity over these frames, in the shape of a track. These tracks can then be either visualized or yield further analysis results such as velocity, total displacement, diffusion characteristics, division events, etc…

TrackMate can deal with spot-like objects or cell-like objects.

• Spots are typically bright objects over a dark background for which the object contour shape is not important, but for which the main information can be extracted from the X,Y,Z coordinates over time. Examples include sub-resolution fluorescent spots, labelled traffic vesicles, nuclei or cells imaged at low resolution.
• Cell-like objects would be objects for which we can retrieve the shape and use it for subsequent analysis.

TrackMate can compute numerical features for each spot, given its coordinates, a radius and its shape. For instance, the mean, max, min and median intensity will be computed, as well as the estimated radius and orientation for each spot, allowing to follow how these feature evolves over time for one object.

TrackMate goals

Its development focuses on achieving two concomitant goals:

For users

TrackMate aims at offering a generic solution that works out of the box, through a simple and sensible user interface.

The tracking process is divided in a series of steps, through which you will be guided thanks to a wizard-like GUI. It privileges tracking schemes where the segmentation step is decoupled from the particle-linking step.

The segmentation / filtering / particle-linking processes and results are visualized immediately in 2D or 3D, allowing to judge their efficiency and adjust their control parameters. The visualization tools are the one shipped with Fiji and interact nicely with others plugin.

Several automated segmentation and linking algorithms are provided. But you are also offered to edit the results manually, or even to completely skip the automatic steps, and perform fully manual segmentation and/or linking.

Some tools for track and spot analysis are included. Various plots can be made directly from the plugin and for instance used to derive numerical results from the tracks. If they are not enough, functions are provided to export the whole results to other analysis software such as MATLAB.

TrackMate relies on several different libraries and plugins for data manipulation, analysis and visualization. This can be a pitfall when distributing a complex plugin, but this is where the Fiji magic comes into play. All dependencies are dealt with by through the Fiji updater. Installing TrackMate is easy as calling the Fiji Updater, and the plugin must work out of the box. If this does not work for you, then it is a bug and we commit to fix it.

A strong emphasis is made on performance, and TrackMate will take advantage of multi-cores hardware.

For developers

Have you ever wanted to develop your own segmentation and/or particle-linking algorithm, but wanted to avoid the painful burden to also write a GUI, several visualization tools, analysis tools and exporting facilities? Then TrackMate is for you.

We spent a considerable amount of time making TrackMate extensible in every aspect. It has a very modular design, that makes it easy to extend. You can for instance develop your own segmentation algorithm, extend TrackMate to include it, and benefit from the visualization tools and the GUI already there. Here is a list of the components you can extend and customize:

• detection algorithms
• particle-linking algorithms
• numerical features for spots (such as mean intensity, etc..)
• numerical features for links (such as velocity, orientation, etc..)
• numerical features for tracks (total displacement, length, etc…)
• visualization tools
• post-processing actions (exporting, data massaging, etc…)

You can even modify the GUI, and remove, edit or insert new steps in the wizard. This can be useful for instance if you want to implement a tracking scheme that solves simultaneously the segmentation part and the particle linking part, but still want to take advantage of TrackMate components.

Do you want to make your new algorithms usable by the reviewers of your submitted paper? Upload your extended version of TrackMate to a private update site, as explained here, then send the link to the reviewers. Now that the paper has been accepted (congratulations), you want to make it accessible to anyone? Just put the link to the update site in the article. All of this can happen without us even noticing.

TrackMate was developed to serve as a tool for Life-Science image analysis community, so that new tracking tools can be developed more easily and quickly, and so that end-users can use them to perform their own research. We will support you if need help to reuse it.

Documentation and tutorials

Downloadable documents and tutorials

• The main manual for TrackMate can be found here:

TrackMate-manual.pdf - 14 MB, 150+ pages.

It contains user tutorials, technical documentation and developer documentation. It compiles in a nice polished pdf the tutorials and information you can find on this wiki, and linked below.

• With TrackMate v7 we introduced several major changes, for which we wrote an additional manual. It can found here:

TrackMate version 7 novelties.pdf - 16 MB, 70+ pages.

Again, it compiles several tutorials and developer documentation also linked below.

Online tutorials

• Getting started with TrackMate is a basic tutorial that explains how TrackMate works on an easy image. You should start here.
• Manual editing of tracks using TrackMate shows how to manually curate and edit tracking results.
• Manual tracking with TrackMate shows how to perform a fully manual annotation of tracks in a source image.
• Keyboard shortcuts for editing contains a summary of the keyboard shortcuts we use here.
• TrackMate v7 new algorithms documents the 8 new detectors introduced with version 7, and the new shape analysis framework. Each subpage contains a tutorial that explains how to use each of the new detector.

TrackMate components

TrackMate has a modular design and ships several algorithms of several types: detectors, trackers, analyzers, etc. The pages below documents individual components, or modules or TrackMate.

• TrackMate Detectors: detect objects in images.
• TrackMate Trackers: link objects to build tracks.
• TrackMate Analyzers: compute numerical values on spots, edges and tracks.
• TrackMate Actions: miscalleneous actions on tracking results.
• TrackMate Views: tracking results viewers.

Interoperability

Python

There are several Python tools contributed by the TrackMate developer community that allows importing TrackMate results in Python and performing track analysis with the libraries of this language. Among them:

• NapaTrackMater https://github.com/kapoorlab/NapaTrackMater by Varun Kapoor, a bridge from TrackMate to Napari.
• pytrackmate https://github.com/hadim/pytrackmate by Hadrien Mary, a Python function that imports TrackMate files in Pandas data frames.
• Single-molecule-tracking-python https://github.com/Colorado-State-University-Stasevich-Lab/single-molecule-tracking-python by the Stasevich lab (Colorado State University), a series of functions in Python to perform single-molecule analysis based on TrackMate results.
• pyTrackMateXMLhttps://github.com/rharkes/pyTrackMateXML by Rolf Harkes, a Python function to follow intensity traces based on TrackMate tracking results.

Please contact their respective authors directly for support.

MATLAB

• Using TrackMate with MATLAB documents the MATLAB functions shipped with Fiji that allows importing data generated with TrackMate into MATLAB.

Scripting TrackMate

• Scripting TrackMate shows how to do tracking using a scripting language, e.g. from the Fiji Script Editor. These example scripts will show you how to use TrackMate as a library and familiarize yourself with the API.

• In scripts, all detectors and trackers are configured in the Settings object using a Map (e.g. in Java) or a dict (e.g. in Python). You need to know the keys of the dictionnary for each detector and tracker, and the type of values they accept. All the keys of the known detectors and trackers are documented in this page.

• Using TrackMate from MATLAB shows how to use MATLAB as a scripting language for TrackMate, and benefit from MATLAB facilities.

Misc information

• TrackMate version history: Please look at the gihub page for TrackMate releases.

• The TrackMate FAQ

• Dave Mason on using pivot tables to get track statistics based on spot features: mean-intensity-of-tracks-using-trackmate

Extending TrackMate

Do you have a tracking or a detection algorithm you want to implement? Of course you can write a whole software from scratch. But at some point you will have to design a model to hold the data, to write code that can load and save the results, visualize them, have even a minimalistic GUI, and allow to manually correct the outcome of your algorithm. This can be long, tedious and boring, while the part that interests you is just the core algorithm.

We propose you to use TrackMate as a home for your algorithm. The framework is already there; it might not be perfect but can get your algorithm integrated very quickly. And then you can benefit from the other modules.

Developer documentation

The subject of extending TrackMate is not completely trivial. However, recent advances in the SciJava package, brewed by the Fiji and ImageJ2 teams considerably simplified the task. It should be of no difficulty for an average Java developer.

This page lists several tutorials show how to integrate a module of each kind in TrackMate. They are listed by increasing complexity, and it is a good idea to practice them in this order.

Known extensions

Some extensions are documented within this wiki. This page lists the documented extensions.

Please tell us if you have one that you want to advertise here!

As Fiji update sites

The Fiji updater already lists several TrackMate extensions as update sites. Their name all start with TrackMate-*:

As much as possible we try to include share their code source on a common GitHub organization dedicated to TrackMate: the TrackMate-SC org.

Downloadable jars

Thanks to continuous integration, the extensions we are aware of are built automatically and can be downloaded following the links below. They point to a simple .jar file that you just have to drop in your Fiji.app/jars folder. TrackMate will recognise the extra modules it ships and will integrate them in the plugin.

Extension name	Content	Authors	Link to jar file	Source code
Find maxima (TrackMate module)	This plugin implements the find maxima detection algorithm for TrackMateas in the Process > Find Maxima… command. The results are almost the same. Subpixel accuracy is activated by default.	Thorsten Wagner	on Github	on Github
TrackMate -> Spot-On connector	This extension adds an action allowing to automatically transfer a tracking analysis performed in TrackMate to Spot-On, without having to export the tracks and reimport them. Spot-On is a web-interface designed for the analysis of single-molecule tracking experiments.	Maxime Woringer	on Gitlab	on Gitlab

Extensions with extra source code

Ronny Sczech TrackMate repository contains the source code to various TrackMate enhancements, in Java and macros.

Extensions documentation

• Find maxima detector from Thorsten Wagner.

Acknowledgements

Libraries

TrackMate actually depends on many other Fiji plugins or libraries. The Fiji Build System system and the Fiji Updater ensures that these dependencies will not bother you. We list them here, with their author when they are not obviously linked:

• ImgLib2 is used everywhere we need dealing with pixels. Relying on imglib made it trivial to have a plugin that deals indifferently with 2D or 3D images. In particular, we use code from Stephan Preibisch, Stephan Saalfeld, Larry Lindsey and Lee Kamentsky.
• ImageJ is of course the entry point for the plugin. We use it display the images as 2D slices and in the HyperStack displayer.
• Internally, the tracks are represented by a mathematical graph. To manipulate it, we take advantage of the excellent JGraphT library.
• TrackScheme, the TrackMate component that is used to visualize and edit tracks uses JGraphX for its UI.
• To display plots and histograms we use JFreeChart.
• Some algorithm in TrackMate rely on the JAMA matrix package.
• Exporting visualizations and analysis results to SVG, PDF and other formats are made through the Batik and iText libraries.
• The TrackMate file format is plain XML, and is generated or loaded using the JDom library.
• For the icons, as almost every ImageJ plugin with a GUI, we used the silk icon set, by Mark James. But we are also very lucky to have icons and logos designed specifically for TrackMate by IlluScienta.

Support

We are extremely thankful for the support of Khuloud Jaqaman while we were implementing in Java a stripped down version of her work on robust LAP tracker, following her seminal paper published in the Danuser group:

doi:10.1038/nmeth.1237

JYT acknowledges funding from the European commission FP7 ICT (project “MEMI”) at the beginning of this project. NP was a visiting student thanks to funds provisioned by the Stanford University. JS acknowledges funding from the Laboratory for Optical and Computational Instrumentation at the UW-Madison and National Science Foundation award #1121998.

TrackMate development uses YourKit as a profiling tool. YourKit supports open source projects with innovative and intelligent tools for monitoring and profiling Java and .NET applications. YourKit is the creator of YourKit Java Profiler, YourKit .NET Profiler, and YourKit YouMonitor.

Who uses TrackMate

It turns out that TrackMate has a decent user base, as exemplified by a crude search on Google Scholar. These citations accumulated before the TrackMate paper was out.