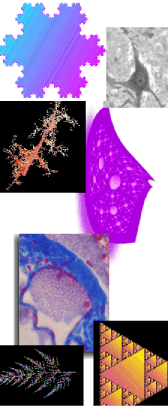
Images must be openable by ImageJ (e.g., jpg, tiff, png, gif), already in or convertible to grayscale or binary format, and amenable to pattern extraction.

Digital Images in FracLac

Images must be converted to RGB or grayscale or else binary before analysis because FracLac counts only certain pixel values. Use FracLac to objectively quantify digital images of:

  • fractals,
  • contours,
  • branching structures (e.g., blood vessels),
  • biological cells (e.g., microglia, neurons, and leukocytes),
  • many other biological structures,
  • textures,
  • and many other patterns and structures.

Image preparation
is important.

Sometimes images are ready for analysis immediately - for binary fractal contours or control images, often the only information in an image is the pattern of interest itself.

But in other cases, pattern extraction may involve considerable preprocessing using ImageJ or other image processing software to threshold, subtract background, dilate, trace or find edges automatically or manually, etc.

The technique to prepare an image for analysis ultimately depends on the feature deemed to be of interest, the type of analysis, and the type of image (e.g., grayscale or binary, contour or texture, etc.).

Extracting Patterns to Analyze with FracLac

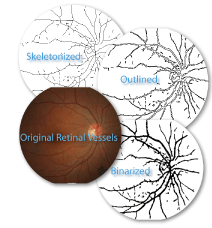First decide which features are important and how you want to study them. The questions being asked determine how images will be prepared. To the left is a group of images showing an original picture of retinal vessels, and 3 alternatives for analyzing the image. To study branching in the retinal vessels in terms of changing length and diameter, for instance, one could convert the retinal image to binary and further to a one pixel wide contour (e.g., using thresholding and ImageJ > Process > binary > Make Binary > Outline). To study vessel branching in terms of length but not diameter, however, one could skeletonize the binarized image (e.g., using ImageJ > Process > Binary > Skeletonize).

Click the image of retinal vessels to see it in higher resolution.

Be aware that the same object may have more than one feature amenable to fractal analysis. In general, binarizing (thresholding to black and white), outlining, etc. are often appropriate if 1) the feature being studied is a contour (a cellular outline, fractal contour, or a control figure such as a circle) and 2) the method being used is a regular box counting scan. However, preprocessing all images using the same set of steps is not always appropriate - as for the images of biological cells shown here, for instance, a method might remove detail that is noise to one investigation but critical to another.


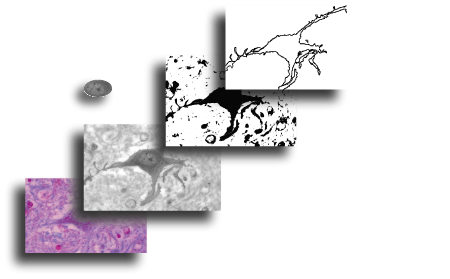
The image shown here, acquired using a light microscope with digital camera attached, illustrates a stained neuron prepared for fractal analysis in two ways, highlighting different features of the same cell that would be studied in different ways.

The series shows the original image (bottom, left), that image grayscaled, the nucleus cropped and extracted for a grayscale texture analysis (left of centre), and the grayscaled image thresholded and outlined to a single pixel wide contour of the entire cell separate from the background for a regular binary analysis (top, right).

Rois

FracLac will analyze selections (rois) on images, so once an image is prepared, relevant rois can be selected and analyzed. For grayscale images, the area outside of the selection will be filled with a filler colour that is ignored by grayscale processing. Grayscale images can be converted to RGB and irrelevant areas filled with non-gray values to tell FracLac to ignore those portions.

Should I use Control Images?

Whenever possible, you should use control images. Although theoretical fractal dimensions do not depend on scale, digital images do and the patterns they represent are imperfect and limited by computer screen resolution and a myriad of other factors. Thus, testing images of known fractal dimension and lacunarity can provide a benchmark for your analyses.

You can make simple contours and shapes (i.e., lines, circles, etc.) easily in most digital imaging software including ImageJ (e.g., in ImageJ, create a new image, select a square or round roi on the blank image, then select ImageJ > Edit > Draw). And you can generate theoretical fractal images using software that lets the user specify line width, level of detail, size, etc. The list below links to some fractal generating plugins for ImageJ freely available from the NIH website, and a free standalone program:

Although the images shown here are illustrated in colour, they can be generated in grayscale or binary formats. You should generate control images in the format (binary or grayscale) they are going to be analyzed in to minimize loss and distortion of information during preprocessing.

Points to Consider

  • For binary scans, use images of comparable size to the ones to be analyzed, showing rectangles, squares, circles, triangles, etc., as well as known fractals and multifractals.

  • Benchmark testing using a standard scan in FracLac is generally 1-5% from theoretical for standard binary images ranging from 100 to 900 pixels in diameter.

  • Larger images tend to be closer to theoretical, and the smallest and most detailed generally deviate most from theoretical.

  • There are practical upper and lower limits on size.

  • Simple contours have a theoretical fractal dimension of 1.0, and filled planes of 2.0. However, a computer screen represents images using a grid of pixels. Thus, circles and angled lines (not horizontal or vertical) are approximated in digital images, and as a result, calculated values of the DB do not always match theoretical for some images. The image below illustrates what happens when a circle is analyzed. At its original size, the circle itself appears round, but as seen in the scaled up image, the curve is approximated by straight segments. On the whole, when the entire image is scanned using box counting, the DB is 1.02, but owing to the limitations of digital images each part of the image is not truly rounded and if considered separately, can be shown to vary from theoretical.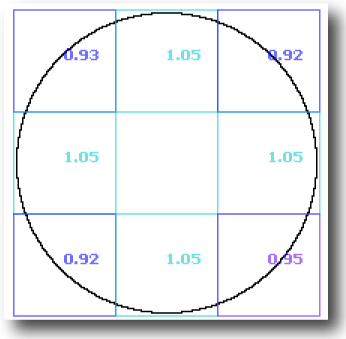

  • Furthermore, owing to the limitations of digital processing and the methods used in FracLac, even a "perfect" filled rectangle can deviate from theoretical. The series of box sizes can be especially important for determining fractal dimensions when scaling relationships are known ahead of time (e.g., FracLac will calculate a perfect 1.00 for a square if it is told the scaling rule ahead of time by setting it to use a series scaled by 1/2, with the maximum box size set to 1/2 the image size at a full integer value and the minimum also set to a full integer value scaled down from that size).

Some limitations of digital images of fractals are discussed in the next section.