-
Using this Page:
- Setting Options:
- Click various options on the screenshot
- Scroll down or jump to the whole list.
- Interpreting Results: Click here
- General Knowledge:
- See the Tips section of this page
- or see the Multifractals page.


This page
explains the options and helps you interpret the results for a multifractal analysis.
Not the page you need? To learn how to use FracLac in general, try the basic tutorial; for a discussion of multifractals, go to the multifractal background page.
The page rather brazenly assumes you know all about using FracLac and have read the background section on multifractals. Cheeky, no? That said, you can click now on one of the three main sections (Options, Results, and Tips) to get on with your business, but, first and foremost, if you have not already, you really should learn about the key to doing a multifractal analysis - the Q.
Q is part of the generalized dimension, D(Q), which is a key variable in multifractal analysis. Q is actually a range of exponents used to calculate and graph all of the variables in a multifractal analysis.
From the perspective of an innocent FracLac user, Q is just an arbitrary exponent—or, as we said, range of exponents—to specify.
The default Q–range is 0±10, incremented by 0.25 You set the maximum, minimum, and increment for the Q-range on the options panel. Experiment with Q settings to see how the multifractal spectra are affected for different images and ranges, but note that, in general, Q<−10 and Q>12 can cause calculation problems.You may have already read about how to calculate the variables, including D(Q) in the multifractals page. Kudos if you can remember all the formulae!
Options
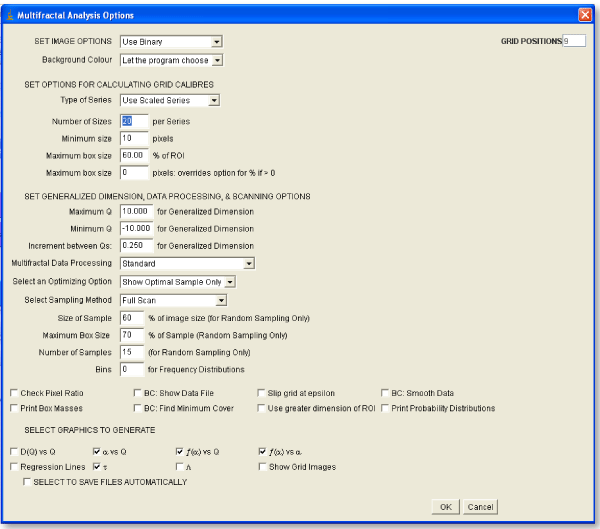
Now that you are primed for the practical part—analyzing—your next step is to click on the screen shot, on whichever options you need to learn about. You can also scroll down or jump to the list. The clickable screenshot shows the actual options panel that comes up for a multifractal scan; to find out how to bring up the panel, go here.
Options List
Results
- Data File See also the Data File page
- Binned Probabilities & Masses File see also the BPD page
- Masses File
Data Files
The results files and graphics returned from a multifractal analysis in FracLac depend on the settings in the options panel. The various data and graphics files from a multifractal analysis scan are listed below. Multifractal Spectra, Calculations, and sampling.
-
Multifractal Spectra Graphics Files
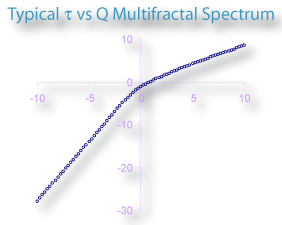
- τ
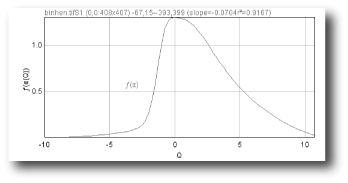
- ƒ(α) vs. α
- ƒ(α) vs Q
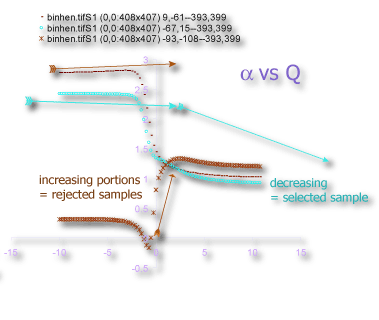
- α vs Q
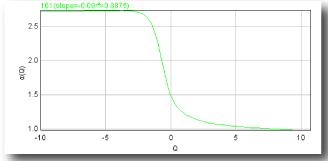
- D(Q) vs Q
Graphics Files
Use the links below to help you interpret the various graphics. All of the graphics are generated by selecting them individually on the options panel. Click on the links to find out about them.The other graphics are explained in the links from the options panel, which you can also access here:
- Other graphics:
Graphics Files
Use the links below to help you interpret the various graphics. All of the graphics are generated by selecting them individually on the options panel. Click on the links to find out about them.The other graphics are explained in the links from the options panel, which you can also access here:
Results Files
-
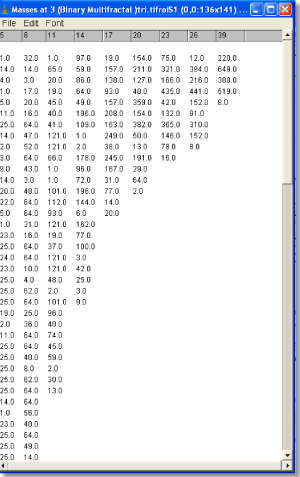
For the Multifractal Results File, click on the column headings in the screen shot or use the links below:
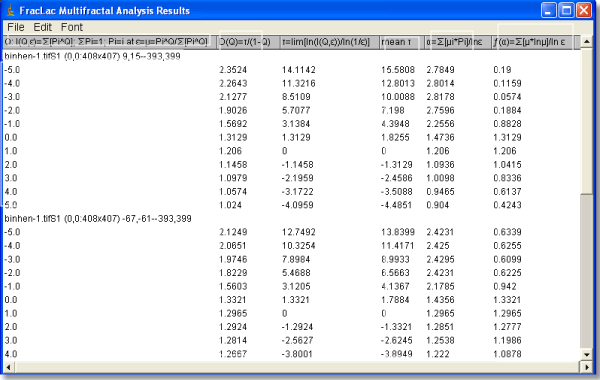 Calculations:
The columns in the results file are calculated as follows:
Calculations:
The columns in the results file are calculated as follows:
- Q = The range of Qs specified in the options panel. Then, the rest of the calculations use the following results from the scan:
- The Generalized Dimension
D(Q)=τ(Q)/(Q-1)
- The τ column
τ(Q) =(Q×α(Q))-ƒ(α(Q))
-
The mean τ (Q) column = the slope of the regression line for ln τ[ε](Q) vs ln ε, where:
τ[ε](Q) = N[ε]-1×N[ε]∑ i=1[(m[i,ε]/M[ε])Q-1]
-
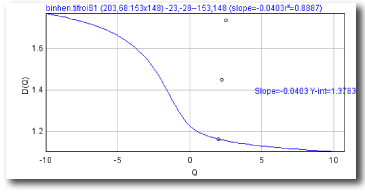
α(Q)
= the slope of the regression line for A[ε](Q) vs ln ε where
A[ε](Q) =N∑i=1 μ[i,ε](Q) × ln P[i,ε]
-
ƒ
(α(Q))= the slope of the regression line for F[ε](Q) vs ln ε where
F[ε](Q) =N∑i=1 μ[i,ε](Q) × ln μ[i,ε](Q)
- Along with each set of 6 columns of data is a filename with numbers to identify the image, slice, roi coordinates and size, and grid coordinates and size. This information is changed and printed before each set. If the optimizer is selected, the set includes rows explaining the selection criteria and how the sample at the specified coordinates met those criteria.
- See Multifractal Calculations
N[ε] = the number of boxes from the box count at some ε
m[i,ε] = mass at any box, i, at ε
M[ε]=N[ε]∑ i=1m[i,ε]
P[i,ε] = m[i,ε]/M[ε]
S[ε](Q)=N[ε]∑j=1(P[j,ε](Q))
μ[i,ε](Q)= P[i,ε]/S[ε](Q)
Tips
The defaults for FracLac's
multifractal scan are set up for a Henon Map (Right click here to download the sample). This may not be an appropriate baseline for your images, however, and you may need to adjust settings accordingly. Following are some pointers that may help if you experience unusual results with multifractal scans, including some workarounds for known bugs.
All Origins are the Same
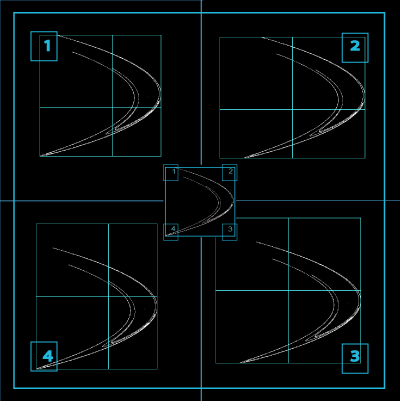
For perfectly square bounding boxes using exact multiples of the bounding box for the largest grid calibre, the first four origins will be identical. This is a bug owing to the way FracLac calculates the first 4 in multifractal scans. A temporary workaround is to select a number higher than 4 to find extra, random origins (e.g., select 8 to get 4 random origins in addition to four identical ones).Unusual Spectra
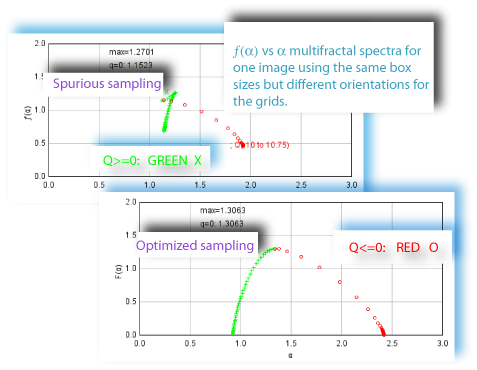
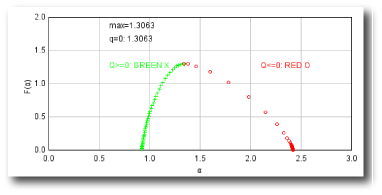
Sampling is usually the problem when your spectra are not quite right. If the graph of D(Q) is not decreasing, or the red and green parts of the MF graph of ƒ(α) vs α do not meet in a continuous curve or appear to cross over as in the example, for instance, sampling may be inappropriate and may reflect a density distribution that attributes too much importance to very small probabilities that appear at some, but not all, grid positions. Negative Qs are most affected. This may simply be a matter of needing to find a better grid orientation, for which the solution is to increase the number of samples, and select to optimize and use a slope-correcting filter. Other potential causes and their fixes are listed below.
Using the Optimizer with Invalid Calculations
If you are using the optimizer, and it appears to incorrectly select such a sample over a better one, there may be calculation errors. This occurs if the values for ± Q are too high. This is a known bug (July 2007) that is being worked on. If it is happening, there will be non-numbers in the some of the results files, and you may see non-numbers (i.e., unintelligble symbols) for "Max=¦¯µ∅ ∑ Σ ¶" printed on the graph of ƒ (α), for instance. A workaround is to try setting the maximum and minimum to a smaller bracket around 0 (e.g., to 5 and -5 instead of 10 and -10, for example).
Invalid Sampling Owing to Problems with Resolution and Grid Calibre
If there are no invalid number errors, increasing the sampling orientations does not correct the problem, and selecting to optimize is also unsuccessful, the minimum resolvable box size may need special attention. To correct this, try changing (usually increasing) the minimum grid size in pixels to a value appropriate for your image. The problem may also be in the upper end of the series, in which case increasing the maximum size or changing the selection at Use Greater Dimension of Roi can help. In some cases, selecting a different series (e.g., switching from scaled series to "default") from the Type of Series box on the options panel will fix the problem. In addition, changing (usually decreasing) the number of box sizes using the Sizes per Series option on the panel may improves the result.
Very Long Processing Time
The number of box sizes can affect your results and processing time. To reduce processing time, it is often helpful to reduce the number of box sizes (e.g., 10 or less). You can select a custom series or a power series, for instance, in the series option on the panel. If you are doing a random mass sample, using less samples or decreasing the sample size may help.
Problems with Random Mass Sampling
If you get strange results with a random mass sample, you may need to adjust the maximum box size as a percent to 100%, adjust the number of box sizes up or down, and ensure the minimum grid size in pixels is high enough (e.g., >5 or 10).

 See
See