NIH Image Engineering |
Index
It is possible to use a scaling system for pixels which has a one to
one correspondence to the concentration of what you are studying. Sample
concentrations can be determined using optical, electronic, and most importantly
for our purposes, a computer based imaging technique. Densitometric science
was described originally by Bouguer and Lambert who described loss of radiation
(or light) in passing through a medium. Later, Beer found that the radiation
loss in a media was a function of the substance's molarity or concentration.
According to Beer's law, concentration is proportional to optical density
(OD). The logarithmic optical density scale, and net integral of density
values for an object in an image is the proper measure for use in quantitation.
By Beer's law, the density of a point is the log ratio of incident light
upon it and transmitted light through it.
OD = Log10(Io / I)
There are several standard methods used to find the density of an object
or a point on an image. Scanning densitometers have controlled or known
illumination levels, then measure transmitted light through an object such
as a photographic negative. Since both the incident and transmitted light
are known quantities, the device can then compute this ratio directly. This
is also the case of those who use a flat field imaging technique and capture
two separate images. The first image is of an empty light box and the second
is of the specimen to be evaluated. These two can then be used in computing
a log ratio.
In the case of a video camera/frame grabber combination, using a non flat field technique, several things are of note. With a camera, you do not measure OD values directly. The camera and frame grabber pixel values are linear with respect to Transmission (T), which is the anti-log of the negative of OD:
T = 10 -OD
or:
OD = -log10(T) = log10(1 / T)
Since this is often a source of confusion among those designing systems
for densitometry you should again note that the camera does not measure
T, nor does it measure OD. Camera systems, CCD's, and any frame grabber
conversion values (pixel values) have been designed so that they are linear
with respect to T. It isn't meaningful to take the minus log of the pixel
value since these are not T values.
Nevertheless, you want to do densitometry and need a scale (not pixel
values) which correlates to concentration or OD. Further, it may not be
convenient to measure the incident light and do a log ratio. Fortunately,
you can use an external standard, such as an OD step tablet or a set of
protein standards on a gel. NIH Image has the built in "Calibrate...
" command to allow you to transform pixel values directly from a scale
which is linear with respect to T and into a scale which correlates to OD
or concentration. The calibrate command, used with standards, is best done
with an exponential, rodbard or other fit since the relationship of OD to
T is not a simple linear (y=mx+b) relationship (see equation above) and
because the camera may not be perfectly linear with respect to T over the
range of density values you use as standards. In other words you have both
created a LUT of OD values for each linear to T pixel value and you help
compensate for slight nonlinearities of the camera.
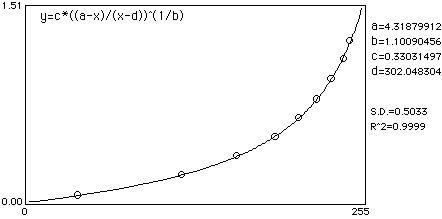
A sample calibration curve fit:

There are several other points of note which you should adhere to in
performing your densitometric analysis. Your standards should always exceed
the range of data which you want to image and perform density measurements
on. You should not use curve fit data (or the pixel values) which extend
beyond the last, or before the first calibration point. Additionally, there
is a point at which the camera can no longer produce meaningful output when
additional light is input (saturation). You could also have a low light
level condition where the camera or CCD can not produce a measurable output
(under-exposure). You will notice that these data points do not fit well
into an end of the curve, or could basically ruin the fit of the data. You
should remove these points from your calibration data and not use the density
values for these pixels in your measurements.
The graph above may help in understanding the relationships involved in densitometric imaging. Along the top we see that transmission and pixel intensity are linearly related. However there is, in reality, a slight non linearity involved as well as under and over exposure factors. On the left, concentration and OD are linearly related. On the right the relationship between OD and T is shown. Fatored all together the image processing system utilzed by NIH Image for densitometry considers these in curve fitting OD to pixel intensity.
References:
If you have a region of interest (ROI) or image area that is calibrated,
such as is done during concentration calibrations, which method for calculation
of a the calibrated mean is preferable:
1) Add up a calibrated value for each pixel in terms of the calibrated
unit, then find the average calibrated unit value and call this the calibrated
mean.
For example:
Calibrated mean = (sum(cvalue(P[i,j])) / N
where cvalue(P[i,j]) is the calibrated value for each pixel in your ROI,
and N is the total number of pixels in the ROI
2) Add up all the pixel values in pixel intensity units, find the mean
pixel intensity value, finally find the one calibrated value for the mean
pixel intensity and call this the calibrated mean.
For example:
Calibrated mean = cvalue(sum(P[i,j]) / N)
where P[i,j] is each pixel intensity in the ROI, and N is the total number
of pixels in the ROI
In an ideal world, it would not make any difference. Both methods would yield the same value However in the real world, measurement and other types of error enter in, and we should think of the problem in a statistical context. If the errors (i.e. the standard deviation) are small, the method used does not matter much. But how small is small? What really matters is the relationship of the standard deviation to the curvature of the calibration curve. If the calibration curve were truly linear, the order of operations would not matter (a property of linear functions). However, in the current context, the calibration curve is always nonlinear, at least in some regions.
The key question then becomes which of the two methods is appropriate
on my data? The answer is it depends. Some cases are clear cut others are
in-between. It is safe to assume that, if you have a fairly uniform gray
level region of interest, where the only variation is caused by the noise
of the imaging process (all noises), method two produces a better estimation
of the mean. In cases where the region contains two highly differing density
regions included in one ROI (the variation is not caused by noise or the
imaging process), then method one produces a better estimation of mean.
The error of method one is directly proportional to the noise of the
system you use and becomes highest when data is measured nearest the asymptote
of the curve fit used to calibrate the data. Most data unfortunately have
some natural density variation and some variation caused by the imaging
process (noise).
Calibration table for step wedge with low noise
40.796 0.05000 118.756 0.21000 159.706 0.36000 189.498 0.51000 207.664 0.66000 221.085 0.80000 231.526 0.96000 240.799 1.12000 246.162 1.26000 249.373 1.40000 251.603 1.55000 252.608 1.70000
Curve fit:
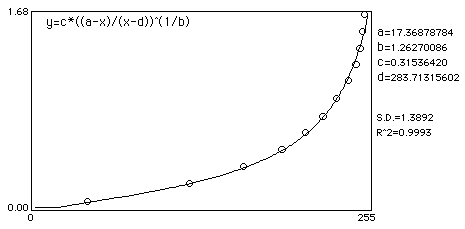
Noise added example
Here is an example which shows how even mild to moderate noise can throw off calibrated mean measurements. In this example, an image of a step wedge is captured. Mean step density measurements are taken after a Gaussian noise with Std Dev of 16 was added and a Rodbard fit was used to fit data to density.
| Actual Mean | Mean Method1 | Error1 | mean Method2 | Error2 |
|---|---|---|---|---|
| 0.05 | 0.048 | 4% | 0.048 | 4% |
| 0.21 | 0.216 | 2.85% | 0.212 | < 1% |
| 0.36 | 0.360 | 0% | 0.353 | 1.9% |
| 0.51 | 0.522 | 2.3% | 0.505 | < 1% |
| 0.66 | 0.677 | 1% | 0.646 | 2.1% |
| 0.80 | 0.845 | 5.6% | 0.788 | 1.5% |
| 0.96 | 1.033 | 7.6% | 0.955 | < 1% |
| 1.12 | 1.192 | 6.4% | 1.120 | 0% |
| 1.26 | 1.308 | 3.8% | 1.224 | 2.8% |
The table above shows that the Error in method 2, on this moderately noisy dataset, is less throughout the range of measurements.
What should I use and what method does
NIH Image use?
What is available in NIH Image? NIH Image uses a slight variation of the first method only in that a histogram is used to do partial sums. i.e.
Calibrated mean = (sum(histogram(n)*cvalue(n)) / N
The histogram helps reduce the error to some degree by decreasing the
number of conversions between pixel and calibrated value.
If you recognize your data as noisy you should consider using the second
mean calculation method. The only current way to do this is use of a macro
in NIH Image, although it contains roundoff error since the cvalue function
only passes an integer.
macro 'Calculate Alternate Mean [C]';
var
nPixels,mean,mode,min,max:real;
begin
SetUser1Label('Mean2');
SetUser2Labe2('%diff');
Measure;
GetResults(nPixels,mean,mode,min,max);
if calibrated then
rUser1[rCount]:=cvalue(round(mean))
else
rUser1[rCount] := mean;
if rMean[rCount] <> 0 then
rUser2[rCount] := (rUser1[rCount] - rMean[rCount]) / rMean[rCount] * 100
else
rUser2[rCount] := 0;
UpdateResults;
end;
Camera signal to noise ratio is defined as the peak to peak signal output current to root mean square noise in the output current. Although this sounds confusing, the value describes whether the camera is one which can give you 256 significant gray levels or not. A formula to convert camera SNR into number of significant digits is very useful. The formula to do this is defined as :
SNR (dB)= 6.02n + 1.8
Where n will be the number of significant bits. You will need 50 or higher
dB for the potential to convert a signal to 8 bits. In practice you will
need a better camera than this to get 8 bits since it is likely most conditions
for imaging are not ideal.
In order to get a true 8 bits, you will also need to capture the video
using a frame grabber that does not introduce error. A frame grabber which
has an analog to digital converter (ADC) with less than one half bit of
differential non-linearity, specified at the video bandwidth, is needed
to capture 8 significant bits.
References:
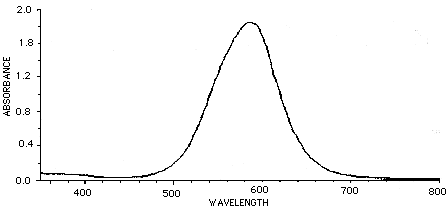
There are filters you can place in front of a camera lens to give complete rejection of the IR (>700nm) wavelengths. This is often crucial in video acquisition using CCD cameras. Filters which show 0% transmittance above 700 to 800 nm are available and recommended over those which show 10% or more transmission at these wavelengths. There are also several filters that compensate for the poor video response in the wavelengths associated with Coomassie blue stains. The graph below represents a pass of Coomassie brilliant blue in typical solution through a spectrophotometer. The peak absorbance is about 585 nm.
Corian Corporation sells filters filters at 630 nm and 560 nm, both of which produce excellent results when imaging Coomassie blue. This is true when sufficient lighting exists. Corian also sells a complete IR suppressing filter for about $200. Filter holders can be purchased at photography stores or fabricated. Tiffen sells 52 and 62 mm ring attachments which fit on typical camera lenses. These are also available at photography stores.
Corian Corp 1-508-429-5065 73 Jeffrey Ave. Holliston, MA 01746-2082 FR-400-S Complete IR surpressing filter P10-630-R and P10-560-R, 630nm and 560nm filters