What is a Fractal Dimension?
Fractal analysis rests on fractal dimensions. There are many types of fractal dimension or DF, all of which measure complexity or the change in detail with changing magnification or resolution.
The animation here shows a koch fractal being generated with increasing levels of complexity.
Scaling Rules
A DF is, in essence, a scaling rule. The rule compares how a pattern's detail changes with the scale at which it is considered - this is what is meant by complexity.
In general, the scaling rule or fractal dimension, D, is found from the general equation N=ε-D where N is the number of pieces and ε is the scale.
To understand the calculations for scaling rules and fractal dimensions, first consider patterns such as the familiar Euclidean shapes of elementary geometry. One shape for which scaling is easy to grasp is a simple line. A line, when scaled by, as an example, 1/3, can be seen to be made up of 3 pieces each 1/3 the length of the original. Thus, D = 1.00 because 3=(1/3)-1. When scaling a filled square by 1/2, similarly, there would always be 4 new pieces, each 1/4 the area of the original, and D would be equal to 2 (e.g., 4=(1/2)-2).
This may seem perhaps trivial, but such straightforward scaling is not necessarily the only kind of scaling that is possible.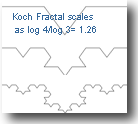
The Koch fractal line illustrated at the left, for example, scales into 4 new pieces each 1/3 the length of the original. In contrast to the line and square considered above, the scaling rule, D, for this figure is not obvious (e.g., 4=3-D).
How is a Fractal Dimension Calculated?
You can calculate a DF by solving the general equation for a scaling rule
which shows that the DF is the ratio of the log of the number of new parts N, to the log of scale, ε:
Note that A is discussed later but is ignored here for convenience.
Practical
- For the simple line mentioned above, the number of new parts is equal to the scale-1, and DF = log 4/log 4 = 1.00.
- For the Koch fractal shown earlier, however, DF = log 4/log 3 = 1.26.
- For the 32-segment quadric fractal on the previous page, the pattern scales into 32 new pieces each 1/8 the size of the previous. Therefore, DF = log 32/log 8 = 1.67.
The �number of pieces� referred to in the above examples is equivalent to the detail in a pattern, and, for the examples given so far, we needed only to count and measure fairly simple features to find the relationship between scale and detail. But it is not always easy to calculate a DF this way because the relationship between scale and detail is not always readily observable. Therefore, methods have been developed to assess the DF indirectly. In practice, the value of complexity is inferred from the ratio of changing detail with changing scale (e.g., magnification or resolution in microscopy) approximated by some measure and assigned a number we call the fractal dimension (DF).
The basic equation for finding a fractal dimension from such data approximating scale and detail where N = the number of new parts and ε = scale is:
DF = lim ε→0[log Nε/log ε]
The limit can be found as the slope of the regression line for the data. The specific methods and calculations used in FracLac are explained in the next section and outlined on the Calculations page.
Note: The fractals discussed here are also called monofractals, to contrast with multifractals.